ARITHMETIQUE & MUSIQUE
La musique est un exercice
d'arithmétique secrète et celui qui s'y livre ignore qu'il manie les nombres.

          Leibniz, 1712.

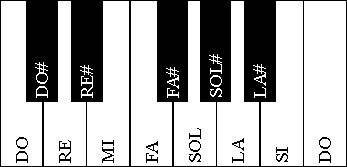
Cliquez sur les notes pour écouter

                         
 

   Les Chinois, il y a 20000 ans, puis les Grecs de l'antiquité avaient déjà découvert les rapports entre les nombres et la musique.
    Ceux qui ont eu la chance, dans leur enfance, d'étudier un peu le solfège ont sans doute encore en mémoire la célèbre suite "FA-DO-SOL-RE-LA-MI-SI" représentant l'ordre des "dièses" qu'il faut aligner à la clef d'une partition, en fonction de la tonalité du morceau.

Mais pourquoi ces notes se suivent-elles de quinte en quinte?

Tout le monde connait par ailleurs la gamme diatonique DO-RE-MI-FA-SOL-LA SI.

Mais pourquoi y a t-il un ton entre DO et RE, mais seulement un demi-ton entre MI et FA ?
Si mon copain Dada savait qu'il fait
des maths chaque fois qu'il sort son
diatonique...
  
 
 
 
Reproduisons ci-dessous l'expérience de Pythagore (soi-même)
(cliquez sur les cordes pour les pincer)
si une corde de longueur L : donne un DO
une corde de longueur 2L : donne un DO plus grave
une corde de longueur 3L : donne un SOL
Les deux premières cordes semblent produire la même note. En réalité, le deuxième DO est à l'octave en dessous. Sa fréquence est deux fois plus petite.
Ecoutons-les ensemble :

Divisons alors la troisième corde par deux pour remonter le son d'un octave. Nous obtenons alors trois cordes de longueurs 1, 3/2 et 2 qui nous donnent les trois notes DO - SOL - DO.
Ecoutons-les:
Les notes DO et SOL "sonnent" bien ensemble. On dit qu'elles sont "accordées".
Le musicien aura reconnu un accord de quinte.
Et si on multiplie de nouveau la longueur de la corde par 3/2, on obtient une nouvelle note accordée avec la précédente (RÉ, LA, MI...). Le problème de cette suite, c'est qu'elle est sans fin. L'idéal serait de retomber sur une corde dont la longueur serait une puissance de 2 de la première, mais cela est impossible, car aucune puissance de trois ne peut être aussi puissance de deux! (Pfou...fallait la sortir, celle-là.)
Il va donc falloir tricher et trouver une puissance de 3 très proche d'une puissance de deux. Suffisamment proche pour que notre oreille ne puisse pas faire la différence. La première répondant à ce critère est 12 (tiens donc...)
3
 12
2 19      
 
ou bien ( 531 441 524 288 )
  
Et voici les douze notes de la gamme
puissance
de 3
/
puissance
de 2
résultat ramené à l'octave
note
obtenue
1
3
9
27
81
243
729
2 187
6 561
19 683
59 049
177 147
531 441
/
/
/
/
/
/
/
/
/
/
/
/
/

1
2
4
8
16
32
64
128
256
512
1024
2048
4096

= 1
= 1,5
/2 = 1,125
/2 = 1,6875
/4 = 1,2656
/4 = 1,8984
/8 = 1,4238
/16 = 1,0679
/16 = 1,6018
/32 = 1,2014
/32 = 1,8020
/64 = 1,6515
/128 = 1,0136

 DO
SOL
RE
LA
MI
SI
FA#
DO#
SOL#
RE#
LA#
FA
retour au DO
Il suffit de ranger les nombres obtenus par ordre croissant pour obtenir la gamme chromatique classique.
 
Mais c'est bien sûr !
Voilà donc le secret de l'emplacement des barrettes de ma guitare !
 
 
   

Mais en réalité, c'est encore plus compliqué que ça !

La note émise par une corde en vibration est en fait constituée de plusieurs:
  - celle de base, appelée fondamentale,
  - et les harmoniques, qui sont en fait des multiples de la fondamentale.
Le nombre et l'intensité des différentes hamoniques détermine le timbre de l'instrument. Et comme si ça ne suffisait pas, pour un même instrument, le panel des harmoniques change en fonction de la hauteur du son.
C'est ce qui rend si difficile (impossible ?) la reproduction fidèle d'un instrument par des moyens électroniques. Mais à quoi bon chercher à imiter un instrument de musique, et se priver du plaisir d'apprendre à en jouer ?
   
C.V.