LE NOMBRE D'OR

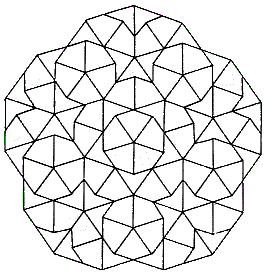
Euclide définissait le nombre d'or de la façon suivante:

Sur un segment AB, plaçons un point P tel que AP/BP = AB/AP .
On a alors AP/BP = , le nombre d'Or, dénommé par lui le "rapport de l'extrême et du moyen".

 
   

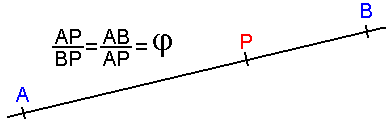
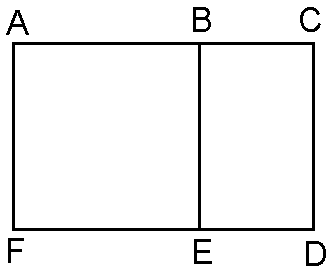
Une autre illustration du nombre d'or, le rectangle d'or:
Si l'on enlève le carré ABEF du grand rectangle ACDF, le rectangle restant, BCDE, a les mêmes proportions que l'original.
Pour trouver le nombre d'Or, donnons à AF la valeur 1, et l'on obtient :

= AC = 1 / BC = 1 / ( - 1)

- - 1 = 0

= (1 + ) / 2 = 1,618033....

 

Depuis Euclide, le succès du nombre d'Or n'a jamais faibli. De la Nature en passant par l'Architecture, les plus grands s'y sont ralliés, tels Léonard de Vinci, qui illustra un ouvrage consacré au nombre d'or, intitulé "La divine proportion". Cet ouvrage décrivait treize constructions géométriques mettant en évidence le fameux nombre.
Dans "Tillings of the plane", paru en 1977, Martin Gardner raconte qu'un ethnologue serait allé jusqu'à décrire la femme idéale comme étant celle dont le rapport entre la hauteur du nez et celle du nombril était égal au nombre d'Or!
Plus ludique, Penrose imagina dans son livre "Pentaplexity"; un pavage basé sur

Ce pavage repose sur l'emploi des deux quadrilatères suivants. Le premier, le cerf-volant, est en fait une portion de décagone. Le deuxième, appelé flèche, complète le premier pour former un losange.
 
   

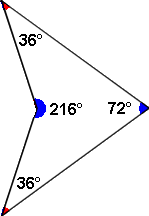
Penrose ajoute un règle de disposition: Les sommets en contact doivent être de même couleur.

    
Il existe une infinité de pavages différents, mais deux seulement admettent une symétrie pentagonale. En voici un ci-contre. Pour trouver l'autre, commencez simplement le centre avec 5 flèches.